前言
最近看了篇文章,了解到了Vector Search。什么是Vector Search?来看看GPT的解释:
向量搜索是一种利用向量表示数据,并基于向量之间的相似性进行搜索的技术。它不同于传统的基于关键词的搜索,能够捕捉数据之间更深层次的语义关系,从而提高搜索的准确性和效率。
相较于基于关键词的搜索,将文本、图片等非数值型数据转换为向量形式,更能发现数据的特征,并发现数据之间的相似性。 至于如何将非数值型数据转换为向量,来开下面这个例子: 用“1”表示“是”,用“0”表示“否”
| 交通工具 | 轮子数量 | 有引擎吗 | 陆地上运动吗 | 最大承载人数 |
|---|---|---|---|---|
| 汽车 | $4$ | $1$ | $1$ | $4$ |
| 自行车 | $2$ | $0$ | $1$ | $1$ |
| 三轮车 | $3$ | $0$ | $1$ | $1$ |
| 摩托车 | $2$ | $1$ | $1$ | $1$ |
| 帆船 | $0$ | $0$ | $0$ | $20$ |
| 轮船 | $0$ | $0$ | $0$ | $1000$ |
把非数值型数据转换为向量,实际上就是把这些数据的特征用数值表示。比如对于汽车来说,它在这个例子中对应的向量就是$(4,1,1,4)$。
基础理论
向量之间的相似性
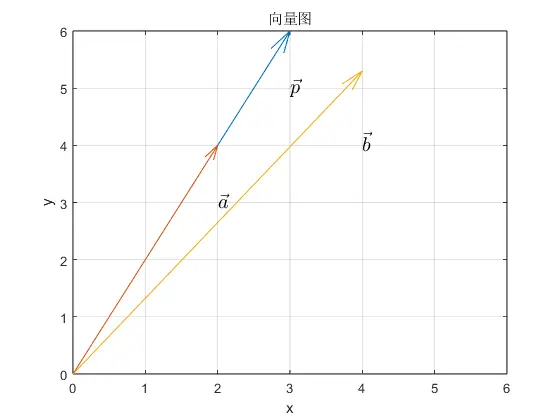 观察向量$\vec{a}$,$\vec{b}$和$\vec{p}$,哪个向量与$\vec{p}$更“相似”?向量$\vec{a}$与$\vec{p}$有着相同的方向,但模长更小;而$\vec{b}$与$\vec{p}$有着相同的模长,但方向只是相近。如果相似指的是方向上的相似,那么$\vec{a}$与$\vec{p}$更相似。而如果相似指的是模长,那么$\vec{b}$与$\vec{p}$更相似。
在矢量搜索中,很少单独根据模长来判断两个向量是否相似。相似性通常取决于方向,或者方向和模长。
观察向量$\vec{a}$,$\vec{b}$和$\vec{p}$,哪个向量与$\vec{p}$更“相似”?向量$\vec{a}$与$\vec{p}$有着相同的方向,但模长更小;而$\vec{b}$与$\vec{p}$有着相同的模长,但方向只是相近。如果相似指的是方向上的相似,那么$\vec{a}$与$\vec{p}$更相似。而如果相似指的是模长,那么$\vec{b}$与$\vec{p}$更相似。
在矢量搜索中,很少单独根据模长来判断两个向量是否相似。相似性通常取决于方向,或者方向和模长。
相似性的评估方法
评估两个向量是否相似,通常有四种数学方法:
- 欧式距离:直接计算两个向量“箭头”的直线距离。
- $d(\vec{a}, \vec{p}) = \sqrt{\sum_{i=1}^{n} (a_i - p_i)^2}$
- $a_i$表示$\vec{a}$的第$i$个分量
- 曼哈顿距离:计算两个点之间沿着坐标轴行走的距离。
- $d_1(\vec{a}, \vec{p}) = \sum_{i=1}^{n} |a_i - p_i|$
- $a_i$表示$\vec{a}$的第$i$个分量
- 点积:将相同维度的分量相乘再相加。
- $\vec{a} \cdot \vec{p} = \sum_{i=1}^{n}(a_i b_i)$
- 余弦值:两个向量夹角的、余弦值。
- $\cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}$ 这四种方法中,欧氏距离是最常用的,而曼哈顿距离与欧氏距离相似,应用这两种方法得到的结果通常也相似。而当需要评估相似性的向量模长一致时,使用余弦值是更好的方法,因为它只与夹角相关。点积与余弦值类似,但在需要大量计算的情况下,点积通常有着更好的性能。
简单的例子
由于在屏幕上呈现二维向量较为方便,因此选取前言中的“轮子数量”与“有引擎吗”作为特征。得到4个向量,分别是$(4,1),(2,0),(3,0),(2,1)$,它们在图上呈现为:
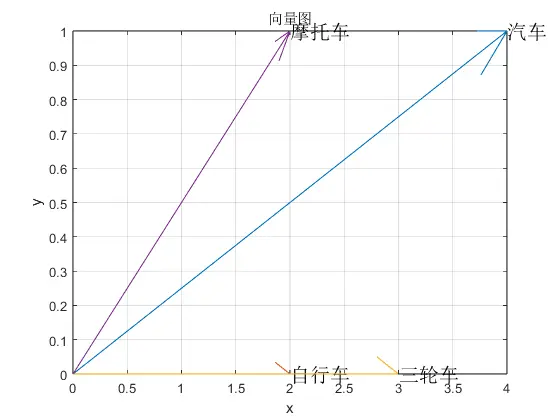 随后分别计算摩托车与自行车、三轮车、汽车的相似性:
随后分别计算摩托车与自行车、三轮车、汽车的相似性:
| 自行车 | 三轮车 | 汽车 | |
|---|---|---|---|
| 欧氏距离 | $1$ | $\sqrt{2}$ | $2$ |
| 曼哈顿距离 | $1$ | $2$ | $2$ |
| 点积 | $4$ | $6$ | $9$ |
| 余弦值 | $0.8944$ | $0.8944$ | $0.9762$ |
可以观察到,无论是欧氏距离、曼哈顿距离、点积还是余弦值,与自行车的“距离”都是最小,而与汽车的“距离”最大。因此,我们可以认为摩托车与自行车是最相似的,而与汽车最不相似。在这个例子中,比较的对象不仅方向不同,模长也不同,因此欧氏距离是最佳的评价指标。
稍复杂的例子
实现K-means聚类算法
实际上,K-means聚类算法正式基于向量间的欧氏距离来实现聚类的。有了以上知识的铺垫,可以动手实现一个简单的K-means算法。具体步骤如下:
- 初始化: 随机选择
k个数据点作为初始聚类中心。 - 迭代:
- 分配数据点: 计算每个数据点到所有聚类中心的欧式距离,并将数据点分配到距离最近的聚类中心所在的聚类。
- 更新聚类中心: 对于每个聚类,计算其中所有数据点的平均值,并将该平均值作为新的聚类中心。
- 判断收敛: 如果新的聚类中心与之前的聚类中心相同(或者达到最大迭代次数),则停止迭代。
- 返回结果: 返回最终的聚类中心和每个数据点所属的聚类标签。 函数代码如下:
def kmeans(X, k, max_iters=300):
n_samples, n_features = X.shape
# 随机初始化聚类中心
centroids = X[np.random.choice(n_samples, k, replace=False)]
for _ in range(max_iters):
# 分配数据点到最近的聚类中心
labels = np.argmin(np.linalg.norm(X[:, np.newaxis] - centroids, axis=2), axis=1)
# 更新聚类中心
new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)])
# 如果聚类中心不再变化,则停止迭代
if np.all(centroids == new_centroids):
break
centroids = new_centroids
# 返回聚类中心和标签
return centroids, labels
应用K-means算法
为了测试上述代码能否正确工作,选择之前打数模的数据集进行测试。首先将数据点画在图上:
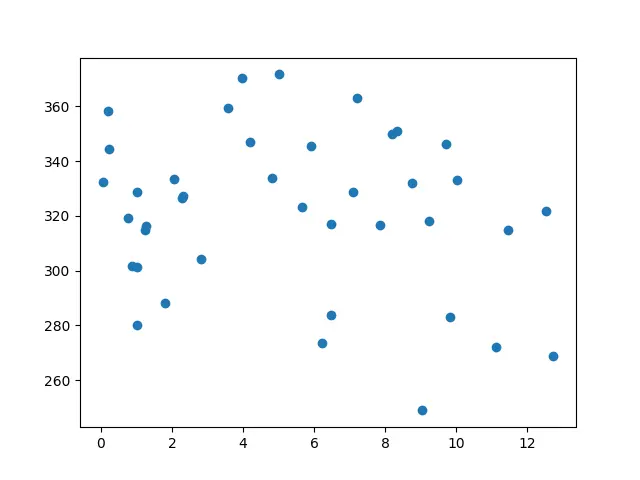 可以观察到有三个聚类簇。应用自己写的K-means算法后得到如下结果:
可以观察到有三个聚类簇。应用自己写的K-means算法后得到如下结果:
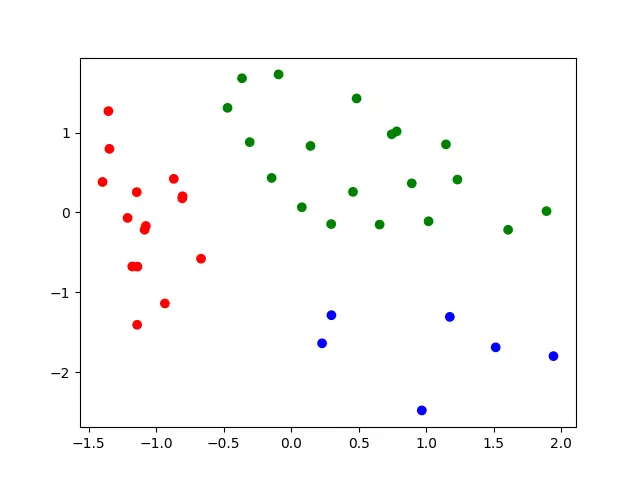 可以看到自己写的K-means算法效果还是不错的。完整代码如下:
可以看到自己写的K-means算法效果还是不错的。完整代码如下:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.preprocessing import StandardScaler
colors = ['red','blue','green'] # 数据点的颜色
def kmeans(X, k, max_iters=300):
n_samples, n_features = X.shape
centroids = X[np.random.choice(n_samples, k, replace=False)]
for _ in range(max_iters):
labels = np.argmin(np.linalg.norm(X[:, np.newaxis] - centroids, axis=2), axis=1)
new_centroids = np.array([X[labels == i].mean(axis=0) for i in range(k)])
if np.all(centroids == new_centroids):
break
centroids = new_centroids
return centroids, labels
# 读取数据并去除异常值,然后标准化
data = pd.read_excel('datas/data2.xlsx')
data = data[['平均的门诊费用','比例']].values
data = data[data[:,0]<500]
scaler = StandardScaler()
data = scaler.fit_transform(data)
centroids, labels = kmeans(data, 3)
plt.scatter(data[:,1],data[:,0],c=[colors[i] for i in labels])
plt.show()
结语
简单了解了一下Vector Search,发现它还是挺有用的。许多聚类算法都是基于Vector Search。之前不甚了解各种聚类算法的原理,只是会调库。这次实践了一下,感觉还是挺有意思的。