线性相位系统的物理意义

考虑一个具有线性相位的理想低通滤波器，其频率响应定义如下：

$$ H_{lp}=\begin{cases}e^{-j\omega n_d},&|\omega|\leq\omega_c\\0,& \omega_c\leq|\omega|\leq\pi\end{cases} $$

对其进行离散傅里叶逆变换，得到它的单位脉冲响应：

$$ h_{\text{lp}}(n) = \frac{1}{2\pi}\int_{-\omega_{\text{c}}}^{\omega_{\text{c}}} e^{-j\omega n_{\text{d}}} e^{j\omega n} \,d\omega = \frac{\sin\omega_{\text{c}}(n-n_{\text{d}})}{\pi(n-n_{\text{d}})},\quad -\infty < n < \infty $$

而一个理想的低通滤波器的单位脉冲响应为：

$$ \frac{\sin\omega_\text{c}n}{\pi n},\quad-\infty< n <\infty $$

可以看出具有线性相位的低通滤波器与零相位的理想低通滤波器的差别只是出现了延时。线性相位的滤波器可以保证信号通过系统后，各种频率成分之间的相对相位关系保持不变。

通常用群延迟$τ(ω)$表征相位的线性：

$$ \tau(\omega)=\mathrm{grd}[H(\mathrm{e}^{\mathrm{j}\omega})]=-\frac{\mathrm{d}}{\mathrm{d}\omega}\left\{\mathrm{arg}[H(\mathrm{e}^{\mathrm{j}\omega})]\right\} $$

一个线性相位的系统，它的群延迟应该是一个常数。

FIR滤波器

原理

$$ H(z)=\sum_{n=0}^{N-1}h(n)z^{-n}=h(0)+h(1)z^{-1}+\cdots+h(N-1)z^{-(N-1)} $$

从系统函数可以看出，FIR滤波器只在原点上有极点，这使得FIR系统具有全局稳定性。FIR滤波器的结构也被称为抽头延迟线结构。

  1. 延迟线（Delay Line）： 指的是用来存储输入信号 $x(n)$ 及其过去的 $N−1$ 个样本的结构。这些样本分别是 $x(n),x(n−1),x(n−2),…,x(n−(N−1))$。这通常通过一系列延迟单元（例如，Z⁻¹ 单元，表示一个单位延迟）来实现。

  2. 抽头（Tap）： 指的是从延迟线上的每一个延迟单元的输出端“抽取”出一个信号。每个抽头都对应输入信号的一个特定延迟版本（例如，$x(n), x(n−1),$ 等等）。

  3. 乘法器（Multipliers）： 每个从延迟线“抽”出来的信号（$x(n−k$)）都会与相应的滤波器系数 h(k) 进行相乘。这些滤波器系数就是 FIR 滤波器的单位取样响应的数值。

  4. 加法器（Summing / Adder）： 所有这些乘法器（$h(k)x(n−k)$）的输出会被汇集起来，通过一个加法器进行求和，从而得到最终的输出 $y(n)$。

特性

相位特性

并非所有FIR滤波器都具有严格的线性相位特性。只有当单位脉冲响应$h(n)$满足对称条件时，FIR滤波器才具有线性相位特性。

图片

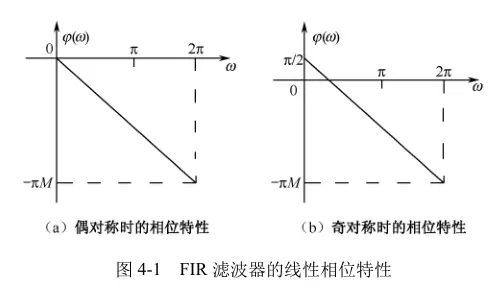
奇对称时，输入信号发生了90°的相移。这种在所有频率上都产生90°相移的变换称为信号的正交变换。

幅度特性

图片

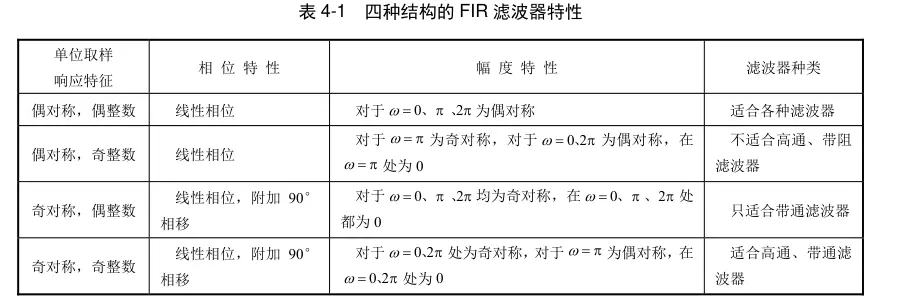
其中“偶整数”、“奇整数”指的是FIR滤波器的长度$N$。

结构

直接型

图片

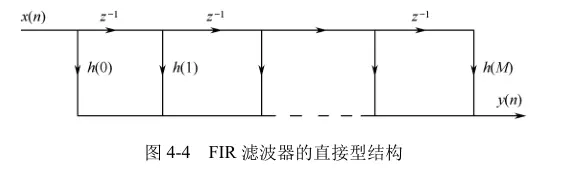
这种结构需要M+1次乘法运算、M个延时单元和1个M+1位宽的加法器。而线性相位的FIR滤波器具有消耗资源更少的结构：

图片

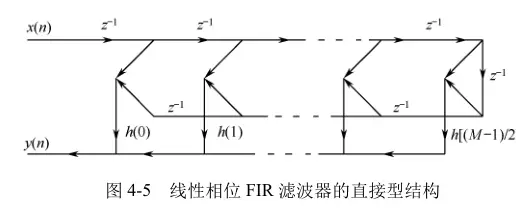
快速卷积型

图片

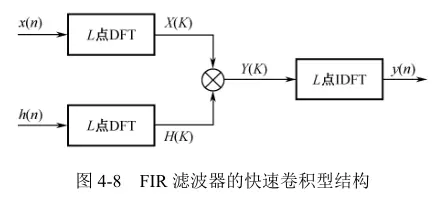
将时域卷积转换为频域相乘，在N、M足够大时，比直接型更快。

另外还有级联型和频率取样型。

FIR滤波器的设计

设计方法

窗函数法

这是最常用也是最简单的方法。基本思路是给出想要的理想滤波器频率响应$H_d(e^{jω})$，然后设计一个FIR滤波器频率响应$H(e^{jω})$去逼近$H_d(e^{jω})$。这种方法是在时域进行的，需要先得出单位脉冲响应：

$$ h_{\mathrm{d}}(n)=\frac{1}{2\pi}\int_{-\pi}^{\pi}H_{\mathrm{d}}(\mathrm{e}^{\mathrm{j}\omega})\mathrm{e}^{\mathrm{j}\omega n}=\frac{1}{2\pi}\int_{-\omega_{\mathrm{c}}}^{\omega_{\mathrm{c}}}\mathrm{e}^{\mathrm{j}\omega n}=\frac{\sin\omega_{\mathrm{c}}n}{\pi n} $$

注意到这个响应是非因果、无限长的。这在实际中是无法实现的，因此需要用有限长的$h(n)$去逼近它。最简单的方法是直接截短$h_d(n)$：

$$ h(n)=\begin{cases}h_\mathrm{d}(n),&\quad-(N-1)/2\leqslant n\leqslant(N-1)/2\mathrm{(}N\text{为奇数)}\\0,&\quad\text{其余}n&\end{cases} $$

窗函数是一种有限长的序列，且只在有限有非零值。将$h(n)$截短的过程可以理解为将它与窗函数相乘：

$$ h(n)=h_{\mathrm{d}}(n)\omega(n) $$

另外还需要将响应变成因果的，可以将它向右平移$(N-1)/2$个采样点。这样可以保证处理后的h(n)具有偶对称性。对于偶对称的FIR系统，它的群延时恰好等于$(N-1)/2$。总之，使用这种方法设计有两点：

  1. 设计一个群延时为$(N-1)/2$的理想滤波器
  2. 使用窗函数截短，截取范围为$0\leqslant n\leqslant N-1$

$H(e^{jω})$能否逼近$H_d(e^{jω})$取决于窗函数的频谱特性（形状），例如矩形窗的频谱特性：

$$ W_{\mathrm{R}}(\mathrm{e}^{\mathrm{j}\omega})=\sum_{n=0}^{N-1}\mathrm{e}^{-\mathrm{j}\omega n}=\mathrm{e}^{-\mathrm{j}(\frac{N-1}{2})\omega}\frac{\sin(\omega N/2)}{\sin(\omega/2)} $$

所有窗函数在频域上都有一个共同的特征：它们具有一个主瓣和一系列旁瓣。

  • 主瓣： 窗函数频率响应中能量最集中的部分，通常是最宽和最高的峰值。
  • 旁瓣： 主瓣两侧较小的、重复的峰值，它们的幅度通常比主瓣小得多，并随着离主瓣中心的距离增加而逐渐衰减。

其中矩形窗的旁瓣是最窄的。

处理完的单位脉冲响应：

  • 间断点变成了连续曲线，因此除了通带和阻带，还出现了过渡带；
  • 旁瓣作用导致幅频特性波动，旁瓣面积越大，通带和阻带波动越大；
  • 增加窗函数长度可以减少主瓣宽度，但不能改变旁瓣和主瓣的相对长度。

常用的窗函数有矩形窗、汉宁窗、海明窗、布拉克曼窗和凯塞窗。

以下是使用各种窗函数分别设计的截止频率为2000Hz，抽样频率为2000Hz的FIR低通滤波器的特性：

图片

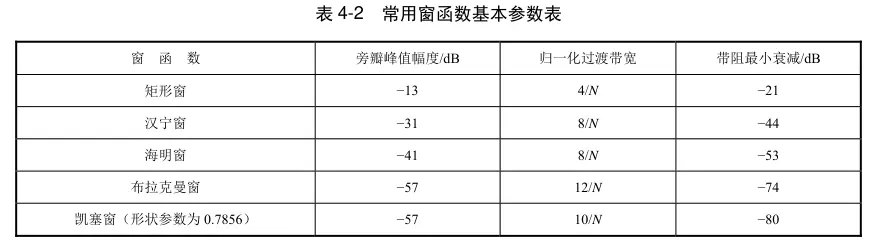
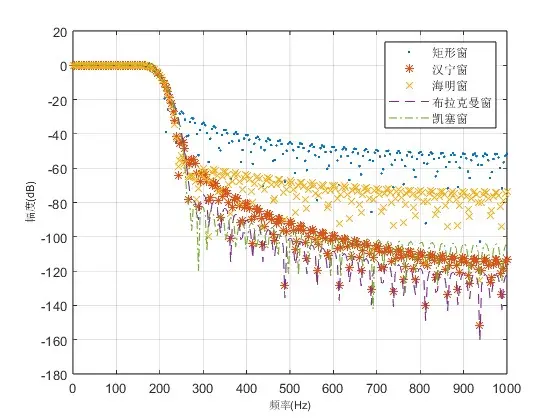
windows

频率取样法

频率取样法设计 FIR 滤波器就是从频域出发，根据频域抽样定理，对给定的理想频率响响应$H_d(e^{jω})$进行等间隔抽样。

$$ H_{\mathrm{d}}(\mathrm{e}^{\mathrm{j}\omega})\mid_{\omega=(2\pi/N)k}=H_{\mathrm{d}}(k),\quad k=0,1,\cdots,N-1 $$

把$H_d(k)$当成待设计的 FIR 滤波器的频率特性抽样值$H(k)$，对其进行离散傅里叶逆变换：

$$ h(n)=\frac{1}{N}\sum_{k=0}^{N-1}H(k)\mathrm{e}^{\mathrm{j}\omega2\pi k/N}\quad n=0,1,\cdots,N-1 $$

在对其进行$z$变换：

$$ \begin{gathered}H(z)=\frac{1-z^{-N}}{N}\sum_{k=0}^{N-1}\frac{H(k)}{1-W_{N}^{-k}z^{-1}}\\H(\mathrm{e}^{\mathrm{j}\omega})=\sum_{k=0}^{N-1}H(k)\phi(\omega-2\pi k/N)\end{gathered} $$

其中$\phi(ω)$为内插函数：

$$ \phi(\omega)=\frac{1}{N}\frac{\sin(\omega N/2)}{\sin(\omega/2)}\mathrm{e}^{-\mathrm{j}\omega(N-1)/2} $$

这种方法较为简单，但内插值依赖于抽样点。如果抽样点之间的理想特性变化激烈，则内插值与理想值的误差较大，在理想特性的每个不连续点出现肩峰和波动。因此这种方式在工程实际中应用较少。

最优方法——等纹波切比雪夫逼近法

纹波切比雪夫逼近法是以加权逼近误差$E(e^{j\omega})$最小为出发点设计滤波器的方法。

$$ E(\mathrm{e}^{\mathrm{j}\omega})=W(\mathrm{e}^{\mathrm{j}\omega})[H_{\mathrm{d}}(\mathrm{e}^{\mathrm{j}\omega})-H(\mathrm{e}^{\mathrm{j}\omega})] $$

以偶对称、奇整数的FIR滤波器为例：

$$ H(\mathrm{e}^{\mathrm{j}\omega})=\mathrm{e}^{-\mathrm{j}M\omega/2}\sum_{k=0}^{(M+1)/2-1}2h(k)\cos\left[\omega\left(\frac{M}{2}-k\right)\right] $$

因为可以通过 FIR 抽样响应的对称性来保证滤波器的相位线性，所以滤波器的设计可以只考虑幅度响应，在误差函数中，可用$\hat H_d(e^{j\omega})$代替$H(e^{j\omega})$：

$$ \hat{H}_{\mathrm{d}}(\mathrm{e}^{\mathrm{j}\omega})=\sum_{k=0}^{(M+1)/2-1}2h(k)\cos\left[\omega\left(\frac{M}{2}-k\right)\right] $$

求解$E(e^{j\omega})$非常麻烦，好在已经有现成的算法：雷米兹算法

FIR滤波器在Matlab中的设计

Matlab中用来设计滤波器的函数有fir1、kaiserord、fir2和firpm等。还有一个用来设计滤波器的图形化工具FDATOOL，用户只需要设置滤波器的几个参数，即可查看滤波器的频率响应、零/极点图、单位脉冲响应、系数等信息。使用这些功能的前提是要在Matlab的附加资源管理器中安装”Signal Processing Toolbox“。

使用FDATOOL设计滤波器

这个工具位于顶部工具栏的“APP”栏目中。

图片

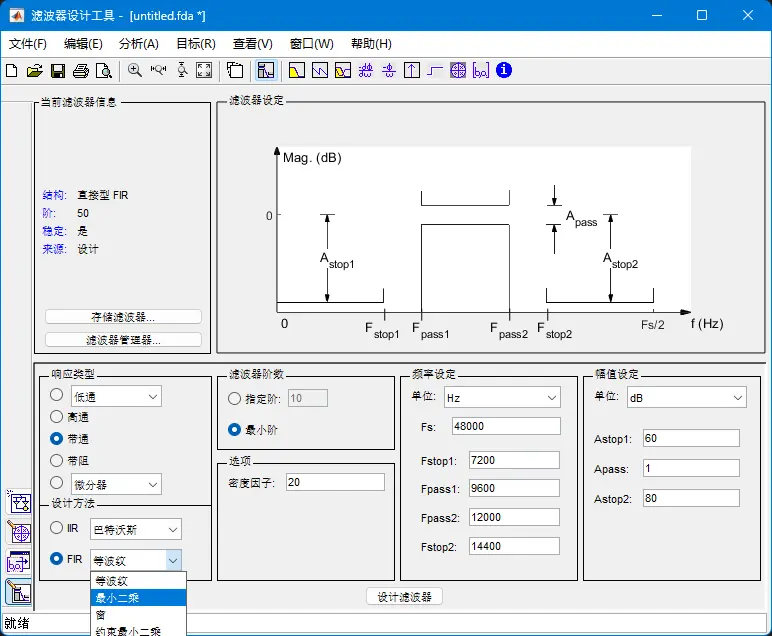
对于等纹波切比雪夫逼近法，“选项”中的密度因子越大，算法在通带和阻带等区域内使用的频率采样点就越多，较高的密度因子可以获得较好的性能，但计算速度会变慢；对于窗函数法，如果选择凯塞窗，可以通过$\beta$系数调整滤波器阻带的衰减，其他窗不行。

工具栏的“分析”中可以查看设计的滤波器的各项指标，如频率响应、零极点图等。“目标”中可以将滤波器系数导出为头文件。