数字滤波器笔记（一）

基础

数字信号处理时常用角频率（$rad/s$)。它和物理频率的转换关系如下：

$$ ω=2π \frac{f_s}{f} $$

其中$f_s$为采样频率，$f$为物理频率。

数字滤波器的分类

经典滤波器

经典滤波器主要包括低通、高通、带通、带阻和全通滤波器。经典滤波器假定输入信号$x(n)$的有效信号和噪声分布在不同频段，当$x(n)$通过一个线性滤波系统之后，噪声能被很好的消减。然而当有效信号和噪声的频带重叠，传统滤波器将无能为力。

经典滤波器的幅频特性响应示意图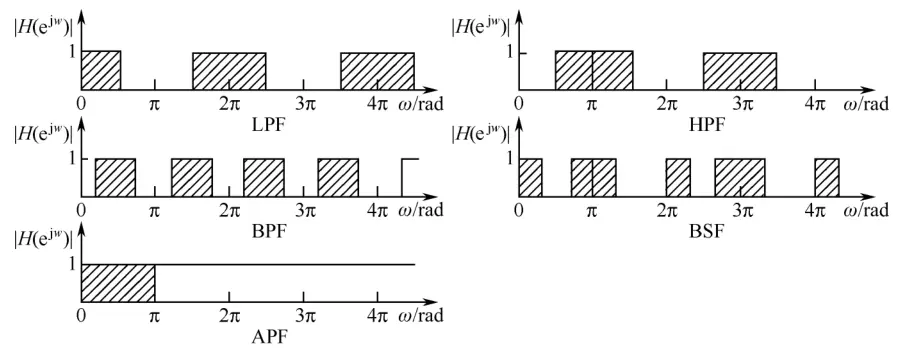：图片

数字滤波器的幅频特性相对于$π$对称，以$2π$为周期。周期性是采样过程的直接结果。当对连续信号进行采样时，信号的频谱会以采样频率$f_s$(对应数字角频率$2π$ 为周期进行延拓和叠加。

现代滤波器

现代滤波器主要包括维纳滤波器、卡尔曼滤波器、线性预测器等。现代滤波器将有效信号和噪声都视为随机信号，并使用统计方法推导出最佳的估值算法。

无限脉冲响应（IIR）

FIR滤波器的输出仅仅是当前和过去输入样本的加权和。它的冲激响应在有限时间内衰减为零。

IIR滤波器的系统函数： $$ H(z)=\sum_{n=0}^{N-1}h(n)z^{-n} $$ IIR滤波器存在反馈环路，不具有线性相位特性，且频率选择性越好的非线性特性越显著。

有限脉冲响应（FIR）

IIR滤波器的输出不仅依赖于当前和过去的输入样本，还依赖于过去的输出样本。它的冲激响应理论上会无限持续下去。

FIR滤波器的系统函数： $$ H(z)=\frac{\sum_{i=0}^Mb_iz^{-i}}{1-\sum_{l=1}^Na_lz^{-l}} $$ FIR滤波器不存在反馈环路，具有线性相位特性。

频域滤波器

有时噪声将在时域下难以处理，如信号频段内的强窄带干扰。然而这种干扰在频域下却很容易识别。频域滤波器正是将信号转换到频域进行处理，然后再转换回时域。

滤波器的特征参数

图片

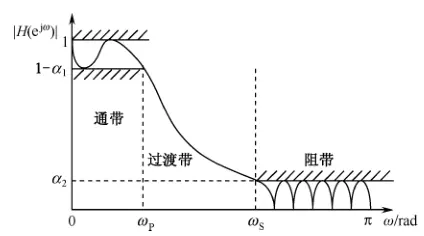
通带内允许的最大衰减$α_p$与阻带内允许的最小衰减$α_s$： $$ \alpha_{\mathrm{p}}=20\lg\frac{|H(\mathrm{e}^{\mathrm{j}\omega_{\mathrm{0}}})|}{|H(\mathrm{e}^{\mathrm{j}\omega_{\mathrm{p}}})|}\mathrm{dB}=-20\lg|H(\mathrm{e}^{\mathrm{j}\omega_{\mathrm{p}}})|(\mathrm{dB}) \\alpha_{\mathrm{s}}=20\lg\frac{|H(\mathrm{e}^{\mathrm{j}\omega_{0}})|}{|H(\mathrm{e}^{\mathrm{j}\omega_{\mathrm{s}}})|}\mathrm{dB}=-20\lg|H(\mathrm{e}^{\mathrm{j}\omega_{\mathrm{s}}})|(\mathrm{dB}) $$ 其中$\mid H(\mathrm{e}^{\mathrm{j}\omega_0})\mid$归一化为$1$。当$\frac{\mid H(\mathrm{e}^{\mathrm{j}\omega_{0}})\mid}{\mid H(\mathrm{e}^{\mathrm{j}\omega_{p}})\mid}=\frac{\sqrt{2}}{2}=0.707$时，$α_p=3dB$，称此时的$ω_p$为该低通滤波器的$3dB$通带截止频率。在信号处理中，3 dB 截止频率通常被认为是信号能量减半的点。

有限字长效应

在数字系统中主要有三种由于有限字长而引起误差的 因素。

  • 模/数（A/D）转换器把模拟输入信号转换成一组离散电平时产生的量化效应；

  • 用有限位二进制数表示系数时产生的量化效应；

  • 在数字运算过程中，为限制位数进行的尾数处理和为防止溢出而压缩信号电平的有限 字长效应。

量化过程可以等效为在无限精度的数上叠加一个噪声： $$ x’(n)=Q[x(n)]=x(n)+e(n) $$

滤波器运算中的字长效应

为什么不增加字长来保证运算过程不产生截尾或者舍入操作？

对于数字滤波器或较为复杂的电路系统来讲，通常会用到反馈网络，这样每一次闭环运算都会增加一部分字长，循环运算下去势必要求越来越多的寄存器资源，长的增加是单调增加的，也就是说，随着运算的持续，所需寄存器资源是无限增加的。

考虑一个一阶数字滤波器，系统函数为： $$ H(z)=\frac{1}{1+0.5z^{-1}} $$ 在无限精度运算的境况下，差分方程为： $$ y(n)=-0.5y(n-1)+x(n) $$ 在定点数运算中，每次乘加运算后都必须对尾数进行舍入或截尾处理，即量化处理，而 量化过程是一个非线性过程，处理后相应的非线性差分方程变为： $$ w(n)=Q[-0.5w(n-1)+x(n)] $$